小初学的容斥原理和高中必考集合的三种运算有什么关系
容斥原理其本质是研究集合间的交叉关系,一般在小学奥数或初中数学学到,而集合则属于高中必考内容,我们初中学过两个实数除了可以比较大小外,还可以进行加减法运算,如果把集合与实数相类比,我们会想两个集合是否也可以进行“加减”运算呢?我们来研究这个问题。

先来理解集合的运算,其一共包含三种:交集、并集和补集。以下逐一展开:
知识点一:集合的交集
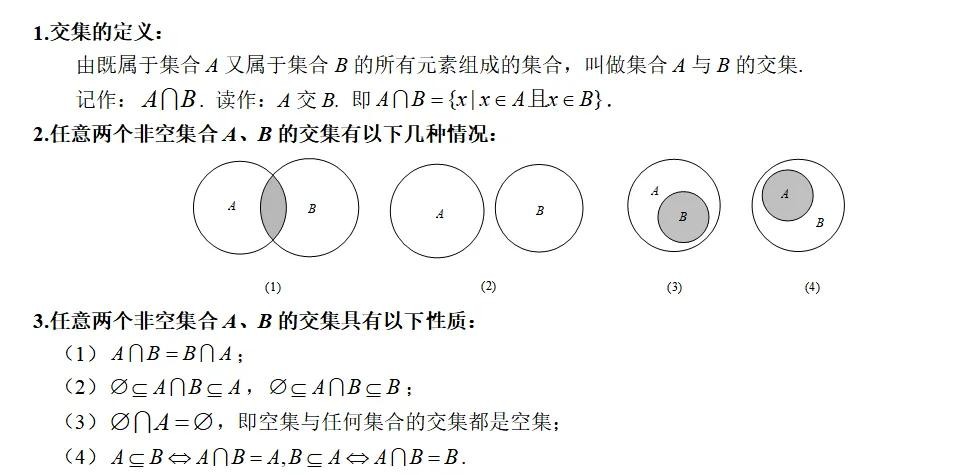
知识点二:集合的并集
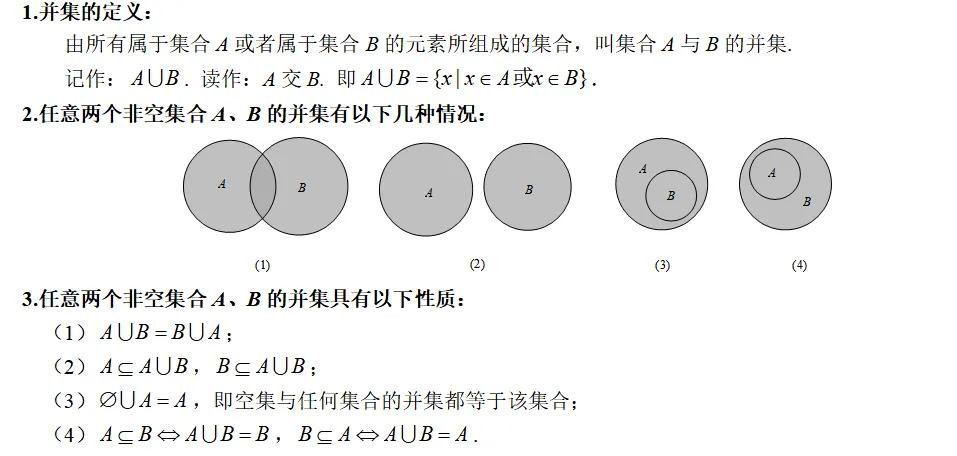
知识点三:集合的补集

知识点四:容斥原理
在计数时,为了没有重复,没有遗漏,使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理.
定义:如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数-既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数.(A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C) .
例如:一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?
分析:依题意,被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分”称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满分的同学”称为“A类和B类元素个数”的总和.为15+12-4=23.
三个集合的容斥关系公式:
|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C|
例:分母是1001的最简分数一共有多少个?
分析:这一题实际上就是找分子中不能与1001进行约分的数.由于1001=7×11×13,所以就是找不能被7,11,13整除的数.
解答:1~1001中,有7的倍数1001/7 = 143 (个);
有11的倍数1001/11 = 91 (个);有13的倍数1001/13 = 77 (个);有7*11=77;
77是11的倍数1001/77 = 13 (个),有7*13=91;91是13的倍数;1001/91 = 11 (个),有11*13=143;143是13的倍数1001/143 = 7 (个).有1001的倍数1个.
由容斥原理知:在1~1001中,能被7或11或13整除的数有(143+91+77)-(13+11+7)+1=281(个),从而不能被7、11或13整除的数有1001-281=720(个).也就是说,分母为1001的最简分数有720个.
以上供参考。

